Einstein’s Miracles, Part 3: Relativity
- Caleb Todd
- Jul 18, 2022
- 13 min read
Einstein’s theory of special relativity is among the greatest scientific works ever produced. The content of his third annus mirabilis paper, On the Electrodynamics of Moving Bodies, constitutes the miracle year’s absolute highest point, and is, to me, the most emblematic of what made Einstein such a transcendent genius. His ability to see the universe with fresh eyes — unburdened by the assumptions built by previous generations — and generate a truly original framework will be shown in full force.
Special relativity challenges our most basic notions of space, time, and motion. We will not be able to fully develop every idea contained in Einstein’s paper, and our approach will diverge somewhat from his to keep things simple. Nonetheless, you will see how fundamental its subject matter is to how we perceive the universe.
Figure 1: Albert Einstein, transcendent genius.
Galilean Relativity
The story of special relativity begins hundreds of years before Einstein with another truly great physicist: Galileo Galilei. Although he is best known for astronomy and heliocentrism, Galileo made significant contributions to the laws of mechanics. In particular, he formulated the socalled Galilean principle of relativity, which constitutes one of two fundamental postulates that Einstein used to derive his theory of special relativity [1]. However, to understand Galilean relativity, we must first take a detour to talk about reference frames.
You can think of a reference frame as the camera through which you are viewing the scene. Imagine someone named Alice is on a train moving at some speed v and passes another person named Bob, who is standing still by the side of the tracks. A camera centred on Bob would see him as stationary and Alice as moving through the shot at a speed v. Conversely, a camera tracking with Alice would see her as stationary and Bob as moving through the shot with a speed v in the other direction. Although we usually think of Bob’s reference frame as being ‘more correct,’ this is only because we spend most of our time stationary with respect to the Earth’s surface. Both perspectives are equally valid.
Suppose Bob is throwing and catching a ball for fitness and for fun. If he throws the ball directly upwards, it will rise and fall without deviating sideways and he will not have to move to catch it. Now imagine that Alice repeats this experiment on the train. She stands still within the carriage and throws the ball directly up. What happens? Does the ball, knowing that the ground is moving beneath Alice, start deviating towards the back of the carriage, forcing her to move to catch it? No. Rather, Alice observes exactly the same behaviour as Bob: the ball rises and falls in a direct line above her. None of the physics changes when you change reference frames. Importantly, that is only true because the train is not speeding up or slowing down as the ball is in the air. Any acceleration will change the result. For that reason, we specifically deal with inertial reference frames — ones which are not undergoing any acceleration. With that established, we can now state the Galilean principle of relativity [1]:
The laws of motion are the same in all inertial reference frames.
In other words, matter has no preferred reference frame; it is impossible to perform an experiment that will tell you which inertial frame of reference you are in. It is very fortunate that this is true, actually. The Earth is hurtling around the Sun at 107 000 kph, so the laws of motion would be very warped indeed in everyday life if it mattered that we were not at rest compared with the Sun (or the rest of the galaxy).
A Not-So-Light Matter
Our story now moves forward a couple of hundred years from Galileo to James Clerk Maxwell — another scientist who is very close to Einstein on the Good-At-Physics leaderboard. Maxwell’s most noted contributions to physics are the so-called Maxwell’s equations that describe the behaviour of the electric and magnetic fields. There is a great deal which can be said about Maxwell’s equations, but for our purposes, only one fact matters: Maxwell used his equations to prove that light is a wave in the electromagnetic field that will travel in a vacuum at the speed c = 300 000 000 m/s [2]. This was a triumphant moment which finally answered one of the most significant problems in physics, namely the nature of light. However, physicists quickly noticed that a major issue arose when Maxwell’s result was applied to the Galilean principle of relativity.
Figure 2: James Clerk Maxwell
Maxwell’s equations are laws of physics, just like Newton’s laws. We know from Galileo that Newton’s laws of motion are the same in all inertial reference frames, so is the same thing true of Maxwell’s equations? If so, that implies that the speed of light (in a vacuum) is c in all reference frames, since the speed of light is a direct prediction of Maxwell. However, this forces us to conclude a seemingly nonsensical result.
Let’s return to Alice, Bob, and the train. If Alice, on the train, is moving at a speed v with respect to Bob, and Alice throws a ball forward at a speed u, then we would naturally expect that Bob sees the ball moving forward at a speed v + u. However, Galileo and Maxwell are now telling us something quite different about light. If Alice, instead of throwing a ball, shoots a beam of light at a speed c, we would expect Bob to see it moving at a speed v + c. However, what the Galilean principle of relativity would claim, if it applies to Maxwell’s equations, is that Bob also sees the beam of light moving at a speed c. This seems like a contradiction. How can the apparent speed of light not change depending on your motion relative to it? Galilean relativity must not apply to Maxwell’s equations. For light, there must be such a thing as a preferred reference frame, and it is possible to detect inertial motion relative to that frame.
Scientists moved quickly to justify why light would have a preferred reference frame. The foremost theory was that electromagnetic waves move through some medium (called the aether), and the speed of light is only c with respect to the reference frame in which the aether is stationary [3]. If so, then the Earth’s motion with respect to the aether ought to be detectable if a sufficiently precise experiment could be devised.
A device known as a Michelson interferometer, named after its designer Albert Michelson, could detect the relative speed of two light waves that travelled in perpendicular directions [4]. If the Earth moves relative to the aether, then a beam of light travelling parallel to the ‘aether wind’ will move at a different speed to one travelling perpendicular to said wind. In 1887, Albert Michelson and Edward Morley built an interferometer that they believed would be precise enough to detect that difference. However, when the experiment was conducted, they detected no absolute aether wind [5]. The Michelson-Morley experiment became perhaps the most famous failed experiment in history.
One candidate explanation for this failure was that the Earth dragged the aether with it, perhaps by gravity. That, however, failed to explain other observations, like the aberration of light. Other explanations were proposed, but there was no satisfying physical interpretation of the experiment. The outcome of the Michelson-Morley experiment (and subsequent repetitions and improvements on it) posed major problems to the physics community. Some of you may be noticing a close correspondence between this story and that of the ultraviolet catastrophe which led Einstein to quantum mechanics in his first annus mirabilis paper: an unexpected experimental result and no satisfactory explanation to be found. All of the best scientific work happens in that space of uncertainty. All of the hardest scientific work, too, but that’s what miracle years are for.
The Two Postulates
While other scientists tried continuously to rework the aether theory to account for the Michelson-Morley null result, Einstein did what he did best: thinking so far inside the box that it sounds like he’s thinking outside the box. Einstein decided to move away from the aether and instead returned to Galileo. He asked himself what would happen if we took Galilean relativity really seriously. What would that imply? He began from just two postulates [6]:
1) The laws of motion are the same in all inertial frames [Galilean relativity]
2) The speed of light in a vacuum is c in all inertial reference frames
[Maxwell’s equations are subject to Galilean relativity]
Thus, special relativity was born. As we shall see, the consequences of these two postulates are patently absurd. But the theory that was born from them has become one of the most precisely verified and universally accepted theories in the history of science.
Figure 3: A laser beam moving from the floor to the roof of a moving train from two different perspectives. Alice sees the light move directly upwards, whereas Bob sees it angled to match the changing horizontal position of the train.
Time Dilation
Let’s return to Alice and Bob. Alice, on the train, has a laser which will send a beam of light from the floor to the roof — a distance of length d. Both Alice and Bob watch this happen and measure how much time the light beam seems to take to travel that distance. In the reference frame co-moving with Alice, which we will call F, the light travels at a speed c, and therefore takes a time t = d/c to travel from the floor to the roof. In Bob’s reference frame, F′, however, the light does not travel directly vertically, but has some horizontal motion as well. If F′ is travelling at a speed v with respect to F, then from Fig. 4 (and using Pythagoras’ theorem) it is clear that Bob sees the light travel a longer distance. We have:
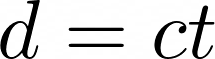
for Alice, but,
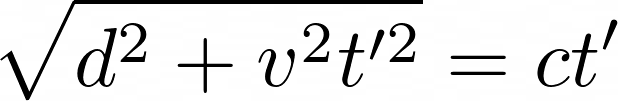
for Bob.
Substituting Alice’s expression into Bob’s and rearranging gives the absurd relation:
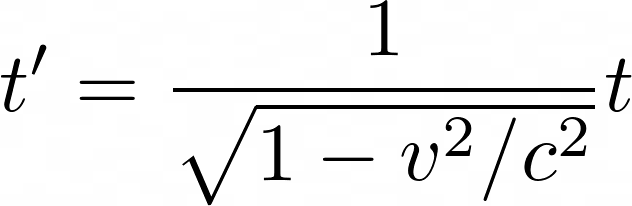
Alice and Bob measure completely different time intervals between the light leaving the floor and hitting the roof. Time is moving more slowly for Alice!
This phenomenon is known as time dilation. The time measured between two events depends on the reference frame you are in. Let us define the factor γ by
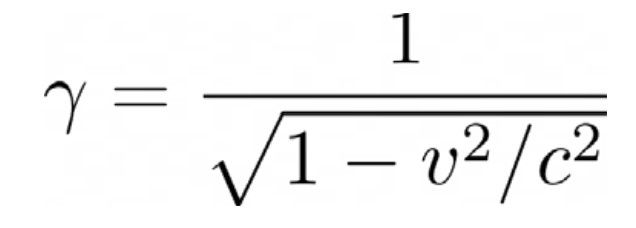
As v increases from 0 to c, γ increases from 1 to infinity. This means the shortest possible time (known as the ‘proper time’) is measured in the reference frame in which the two events are stationary (where v = 0) — Alice’s frame, in our example. Any other reference frame will measure a longer time interval (since v ≠ 0 implies γ > 1), and the greater the relative velocity between reference frames, the longer the time interval will be.
Time dilation is a shocking reality to confront. If you had a twin who became an astronaut and travelled to Alpha Centauri at a speed close to the speed of light, the journey would seem to take around four years to you, but they may have only experienced a few weeks. You would still be twins, but no longer the same age.
Interestingly, time dilation is a phenomenon that may allow us to feasibly colonise incredibly distant planets. If we find a planet on which humans could live but which is thousands of lightyears away, it would seem impossible for us to reach it before the colonists on the spaceship died. However, due to time dilation, a thousand-year journey could constitute just a few hours of a colonist’s life if the ship were fast enough. Unfortunately, those on Earth would not live long enough to find out if the ship arrived at its destination, unless our lifespans increased by a couple of thousand years.
Length Contraction
The bending of reality does not end with time dilation, though. Now let’s imagine that Alice and Bob both try to measure the length of the train. To do that, they both measure the time taken for the entire train to pass Bob. Alice gets:
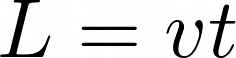
and Bob gets:
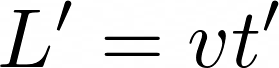
But remember that t and t′ are not the same. This time, our two events are the front and back ends of the train passing Bob. These two events happen at the same place in Bob’s frame, so he measures the proper time.
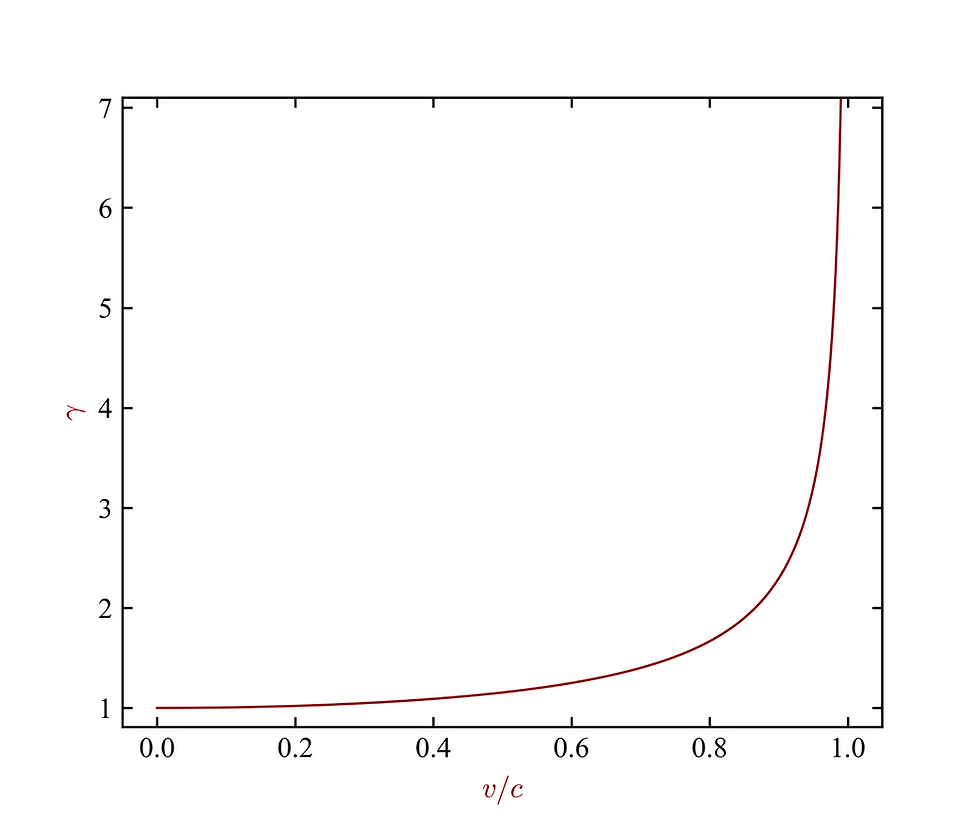
Figure 4: A plot of γ (known as the Lorentz factor) against reference frame speed as a fraction of the speed of light. The larger γ becomes, the more distorted space and time are when compared across reference frames
Alice, therefore, measures a time lengthened by a factor of gamma. Substituting that relationship into these two length equations yields:
So the size of an object — the distance between two points — depends on the reference frame as well. The longest possible length (known as the proper length) is measured in the reference frame in which the object is stationary — Alice’s frame, where the train is motionless. The object’s length in any other reference frame is shortened by larger and larger proportions as the relative speed between reference frames increases. This is length contraction.
Velocity Transformations
As we have seen, both time and space are distorted when comparing inertial reference frames. We must expect, then, that the velocity of an object (how quickly its position changes as time increases) will also defy our intuition. If Alice throws a ball forward on the train at a speed u, at what speed u′ will Bob measure it to be travelling? Pre-Einstein, the answer would be u + v. Post-Einstein, however, the answer becomes something more bizarre:
This equation has an important consequence. If Alice throws the ball at the speed of light, i.e., if u = c, then the speed Bob measures is:
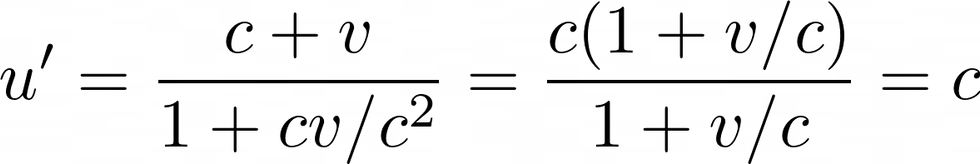
In other words, something travelling at the speed of light in one reference frame is travelling at the speed of light in any reference frame. This was one of our postulates, so we are seeing that the theory of special relativity is self-consistent. Furthermore, any speed u in any reference frame v will always be measured as less than the speed of light. There is a universal speed limit: c. Nothing can travel faster than the speed of light.
Simultaneity and Causality
With time and space now fully bent — and our brains bent with it — let us now turn to a thought experiment that brings to light an apparent contradiction in special relativity. Alice’s train hurtles towards a tunnel that is half the length of the train. At each end of the tunnel are enormous guillotines that Bob can control and which would destroy the train if it were in the wrong place at the wrong time. When Bob sees that the train is exactly in the middle of the tunnel, he drops both guillotines simultaneously, but finds that nothing at all happens to the train. How can that be the case? Well, fortunately for Alice the train was travelling at 90% the speed of light, so length contraction meant the train was less than half its proper length (and therefore able to fit entirely within the tunnel) in Bob’s frame of reference.
That sounds all fine and dandy, given what we know about special relativity. The contradiction, however, comes when we try to view the same situation in Alice’s frame instead of Bob’s. In her frame, the train is stationary, and therefore its length is not contracted. Furthermore, the tunnel is moving towards her at 90% the speed of light, and therefore it is contracted to less than half its proper length (i.e., less than 1/4 the length of the train). There is no way for the train to fit entirely inside the tunnel, and therefore it is impossible for it to survive when the guillotines drop simultaneously. It would seem, then, that Alice sees her train being cut into pieces. How can the train be destroyed according to one observer, but remain unscathed according to another? Though different observers will perceive space and time differently, they must surely agree on what actually happens to the train, right?
Figure 5: Ten years after inventing special relativity, Einstein would take the idea of spacetime even further. His general theory of relativity describes gravity as curvature in spacetime, leading to diagrams such as this (acquired from pngwing.com).
The resolution of this paradox comes by challenging something I implicitly assumed in my description of what Alice sees. Just because the two guillotines drop simultaneously in Bob’s reference frame does not mean they drop simultaneously in Alice’s reference frame. Alice survives in her own reference frame because she sees the far guillotine drop first (before she reaches it), then a pause before the rear guillotine drops after she has passed it by. The order of events can depend on the reference frame through which they are viewed! The concept of time in special relativity is entirely different to what we normally experience. There is no absolute ‘present’ across all reference frames, and different observers can disagree on the order in which events occur. This is the relativity of simulteneity.
The final complication to this rearrangement of events is causality. If one event causes another, their order cannot be switched. Fortunately this is accounted for in special relativity via the universal speed limit c. It is only possible for one event to cause another if a signal travelling at the speed of light (or slower) can leave the first event and reach the second one on time. If they are too far apart, no information about the first event can influence the second. The maths of special relativity says that the order of two events can only be switched if a beam of light could not travel between them, so causality is preserved.
Spacetime
Throughout this article, I have been referring to space and time separately, but almost always in conjunction. PreEinstein, space and time were viewed as entirely disjoint entities. However, the more you learn about special relativity, the more linked these two aspects of reality become. Indeed, Einstein’s third annus mirabilis paper unified them through the concept of a spacetime interval.
Before special relativity, we believed that distances were the same no matter what reference frame you were in. If two objects are separated by distances x, y, and z in the three spatial dimensions we experience, then the value r 2 = x2 + y2 + z2 was invariant across frames of reference. However, we now know that length contraction exists and therefore the Euclidean distance r is not preserved. As length is contracted, though, time is dilated. So, Einstein was able to discover a new value called the spacetime interval between two events, s2 = t2 - x² + y² + z2 , that was the same in any reference frame. The spacetime interval replaces the notion of distance in special relativity. Space and time were no longer separate entities, but rather two parts of a larger fabric of spacetime. This is why we now say that we live in a four dimensional universe, as opposed to three.
Spacetime addresses the interesting oddity in special relativity that is the universal speed limit. It seems strange that any speed is possible less than c, but nothing can move faster. It’s almost asymmetrical in that way. When space and time are unified, though, a rather pleasing resolution to that awkwardness manifests itself. We know that the faster a reference frame is moving, the more slowly time is passing in that reference frame. In other words, the faster something moves through space, the slower it moves through time. So, it is not really the case that any speed is possible; instead, there is only one speed. Some objects are stationary and are moving forward through time at a ‘speed’ c, while others are using some of their speed to move through space instead, and hence move more slowly through time. Everyone and everything is travelling at the speed of light, just in different directions.
Not the End
This article is overly long already, yet I haven’t even covered half of what Einstein spoke about in his paper, nor was this the last paper he wrote on the subject. Furthermore, you may have been wondering why we call special relativity "special" relativity, not just relativity. The answer is that special relativity is merely a special case — a subset — of the more general theory of general relativity, which also incorporates non-inertial frames of reference. General relativity was unleashed on the world by Einstein in 1915 and has become, along with quantum field theory, one of the two pillars of modern physics. Without special relativity, though, general relativity would not have been possible.
Special relativity is an extraordinary topic that forces you to really think like a scientist — casting off your assumptions. We are now three papers into Einstein’s ‘miracle year’, and it is becoming increasingly clear why 1905 is now known by that name. The fourth and final annus mirabilis paper will be an elaboration on some aspects of special relativity which we have not mentioned, notably giving rise to the most famous equation in history: E = mc2 . That will be the topic of my next article here in UoA Scientific.






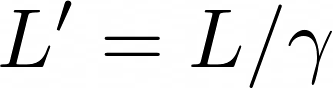






Comments