Mysteriously Massive Muon Magnetic Moment Might Mean Missing Maths

Kevin Stitely

Image from Wallpaperbetter

In 2013, a huge effort was taken to transport a giant 15 m wide superconducting electromagnet over 5,000 kilometres from Brookhaven National Laboratory in New York, to FermiLab National Accelerator Laboratory in Illinois, in the United States. The trip took 35 days of painstaking care, as even a few degrees of bending the extremely sensitive equipment would cause irreparable damage.

The magnet was being moved in preparation for a series of experiments aimed at probing a fundamental particle called the muon, the electron’s more massive cousin. The magnet is used to maintain an extremely uniform magnetic field inside of which a beam of muons travels in a circle at nearly the speed of light. The experiments aim to measure a tiny wiggling motion that the particles undergo when subjected to a magnetic field, which might tell us something about the fundamental structure of matter.

Fig. 1. The Muon g-2 storage-ring superconducting electromagnet nearly arriving at FermiLab National Accelerator Laboratory. Photo from FermiLab Creative Services.

According to the theory of quantum electrodynamics (QED), particles with a peculiar property called “spin” behave as tiny, tiny bar magnets, with a strength described by their so-called magnetic moment, which is often quantified in terms of their “g-factor.” Particles which possess spin will undergo a sort of spinning-top-like motion when in the presence of a magnetic field, called precession. The magnetic moment of the particle then dictates the speed at which the particles precess. The prediction and subsequent measurement of the g-factor of the electron then became one of the first precision tests of the theory of QED. The first theoretical calculation was performed by Paul Dirac nearly a century ago, where he noted a value of exactly two [1].

Figure 2. Schematic of the Muon g-2 experiments.ure

The calculation depends on how electrons interact with photons, quantum particles of light. Dirac used the simplest (relatively speaking) possible interaction, but as quantum theory was further developed it became clear to physicists that there was more to the story. As well as the particles already being considered, namely an electron and a photon, there are also “virtual” particles that can, briefly, appear out of the fabric of space itself to provide additional interaction pathways. Interactions with virtual particles of the so-called vacuum field cause the g-factor of particles to be ever so slightly larger than two. The part of the g-factor that is the result of these virtual particles is then g-2, which quantifies the extent of the particle’s interaction with the vacuum field. The corresponding modification to the magnetic moment is called the anomalous magnetic moment. The theoretical calculation of the anomalous magnetic moment of the electron was carried out by Julian Schwinger in 1948 [2], and stands as a contender for the most accurate prediction ever performed in all of science, with over ten significant figures of agreement with experimental results. The result is engraved on Schwinger’s tombstone.

The story is similar for the muon. The bare calculation without the interactions of virtual particles again yields g = 2, and the inclusion of virtual particle effects slightly increases the value. However, the muon is much more massive than the electron, and therefore interacts with virtual particles in the vacuum more strongly. This is the key reason behind the interest in the magnetic moment of the muon specifically. Whilst the virtual particles that the electron interacts with are primarily photons, the muon features virtual interactions with a much wider class of particles that result in the weak nuclear force, called neutrinos and W and Z bosons. These particles are responsible for the stability of atomic nuclei. Interactions of the muon with virtual W and Z bosons cause a further increase to the anomalous magnetic moment, and make the theoretical calculations of the g-factor of the muon much trickier.

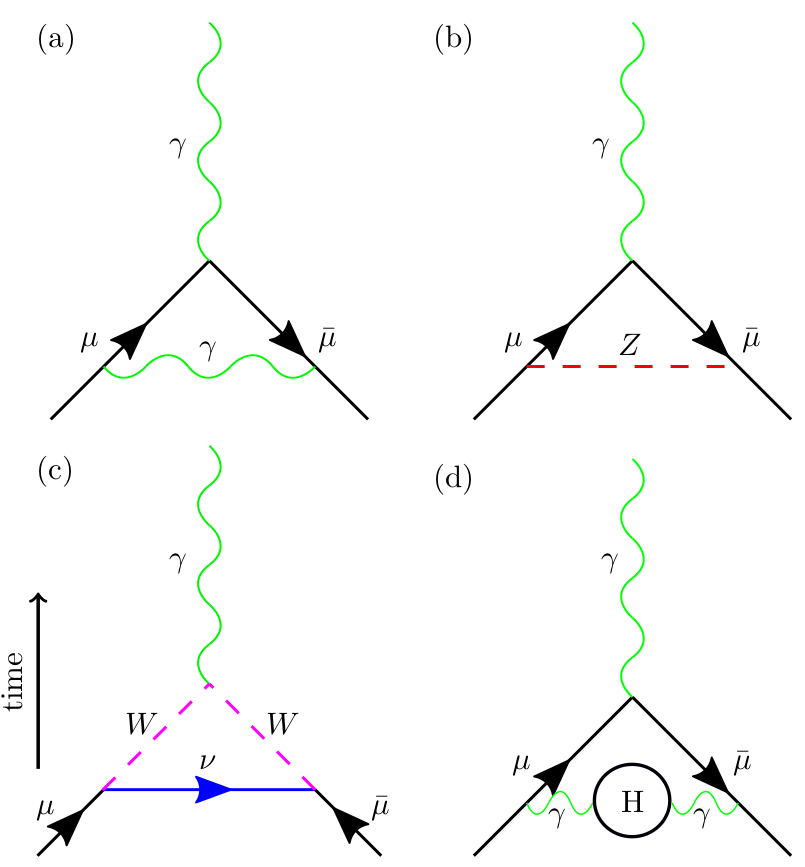
Figure 3. Example Feynman diagrams of muon interactions via QED (a), weak interactions (b) and (c), and interaction with virtual hadrons (d).

Illustrations of some of the most basic types of particle interactions that the muon can experience are shown in Fig. 3. The diagrams, called Feynman diagrams, show particles as lines incoming and undergoing interactions where lines meet. The simplest virtual particle interaction in QED is shown in Fig. 3(a). Here a muon mu and an antimuon mu(bar) (the muon's antiparticle) exchange a virtual photon gamma before colliding and annihilating, creating another photon gamma. These are the types of interactions that cause the anomalous magnetic moment in the electron. The muon, on the other hand, is also more strongly affected by interactions of particles belonging to the weak nuclear force, W and Z bosons. Two of these possible interaction pathways are shown in Fig. (b) and (c). As well as interactions mediated by the weak nuclear force, there are also effects brought about by another fundamental force - the strong nuclear force. This force is associated with composite particles called hadrons, such as protons and neutrons. As shown in Fig. 3(d), the strong nuclear force contributes to the anomalous magnetic moment of the muon via the creation of virtual hadrons.

The first results of the experiments were published this April [3]. The results of the muon g-factor, along with the currently accepted theoretical value [4], are

g theory = 2.00233183620 +/- 0.00000000086

g experiment = 2.00233184121 +/- 0.00000000082

While the difference between the theoretical prediction and the experimental result may seem extremely close, the experiments are so incredibly precise that the observed difference here is significant. The important question that scientists are asking now is: is the difference significant enough? The difference observed here is 4.2 standard deviations, meaning that the probability of observing such an extreme result by chance is roughly 1 in 40,000. However, the currently accepted standard in particle physics to mark the discovery of new physics is 5 standard deviations difference, which represents a probability of about 1 in 2 million.

The currently observed discrepancy between theory and experiment, which is in agreement with previously obtained experimental values from Brookhaven National Laboratory [5], is very exciting for physicists hoping that this could be an early indication of physics beyond the Standard Model. The Standard Model of particle physics is our current de facto understanding of the quantum world. It includes the quantum theory of electromagnetism (QED), the weak nuclear force, and the strong nuclear force. The idea here is that the theoretical calculation, which includes all known interactions given by the Standard Model, could be missing either some interactions between particles already known to exist, or is missing contributions from particles as yet unknown. Either case would give rise to a wealth of new physics and would glean new insight into the fundamental constituents of matter.

There is, however, another camp of theorists which contends that the experimental results of Brookhaven and FermiLab can indeed be calculated via the Standard Model. The issue here comes down primarily to the muon interactions with virtual hadrons, such as illustrated in Fig. 3(d). In any theoretical calculation of interactions of fundamental particles with the vacuum field, each and every interaction pathway cannot be accounted for, as there are actually infinitely many of them. Instead, only the most important types of interactions are considered. This approach, called perturbation theory, works excellently in the case of the electron because the more complicated the interaction pathway, the smaller the contribution. As a result, only finitely many of them need to be calculated and the rest can be thrown away if the role they play is so small they won't be detectable anyway. However, this situation is more complicated in the muon because the strong nuclear force, which governs how the hadrons interact, cannot be calculated in a perturbative manner. Instead, theorists resort to using data-driven approaches that use results gathered from previous experiments to estimate contributions of hadronic interactions [4]. This is the main source of uncertainty in the theoretical predictions of the muon magnetic moment.

In a paper published the same day the FermiLab experimental results were unveiled [6], a team of theorists known as the BMW collaboration (so-called because of the cities most of the physicists are from - Budapest, Marseille, and Wupppertal) revealed a new theoretical calculation of the anomalous muon magnetic moment based on the Standard Model using lattice quantum field theory. Usually quantum field theories treat spacetime as a continuum which is infinitely divisible — at least to wherever our current theories fail. Instead, lattice quantum field theory treats spacetime as an extremely fine mesh of gridpoints, with particles only allowed to exist on points, not the spaces in between. This allows for forces such as the strong nuclear force to be simulated on a (very large) computer in a brute-force fashion. Using this procedure, the BMW team calculated a value for the muon magnetic moment that appears to be much closer to the experimental results than the currently accepted theoretical prediction using the data-driven approach. This suggests that the currently observed discrepancy between theory and experiment could be reduced with Standard Model physics alone.

In conclusion, the results as they currently stand are inconclusive. They recently divulged measurements of the muon magnetic moment of FermiLab align remarkably with previously established results taken at experiments in Brookhaven. The results indicate a discrepancy between the experiments and the theoretical predictions offered by the Standard Model, but not to an extent that can definitively be called statistically significant to the standard set in particle physics. Nonetheless, there are high hopes that there is physics outside the Standard Model to be found in the muon. The situation is further muddled by suggestions that with the different computational methods offered by lattice quantum field theory, the current experimental observations can be adequately explained by the Standard Model. As of right now, the scientific community is yet to reach a consensus until theoretical and experimental techniques are honed over the coming decades. In either case, the stage is set for a wealth of new physics to be discovered as a result of the curiously large muon magnetic moment.

References

[1] P. A. M. Dirac, “The quantum theory of the electron. Part II,” Proc. R. Soc. A, vol. 118, no. 351, 1928.

[2] J. S. Schwinger, “On quantum electrodynamics and the magnetic moment of the electron,” Phys. Rev., vol. 73, no. 416, 1948.

[3] Muon g-2 Collaboration, “Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm,” Phys. Rev. Lett., vol. 126, no. 141801, 2021.

[4] T. Aoyama et al., “The anomalous magnetic moment of the muon in the Standard Model,” J. Phys. Rep., vol. 887, pp. 1-166, 2020.

[5] Muon g-2 Collaboration, “Final report of the E821 muon anomalous magnetic moment measurement at BNL,” Phys. Rev. D, vol. 73, no. 072003, 2006.

[6] S. Borsanyi, et al., “Leading hadronic contribution to the muon magnetic moment from lattice QCD,” Nature, vol. 593, pp. 51-55, 2021.