Photon Statistics of an Open Quantum System with a Quantum Feedback Loop

Alex Chapple

Individual particles of light, known as photons, are instrumental in developing quantum information technologies and quantum computers, the last of which I'm sure you've heard of. Quantum technologies promise a lot (which you can read all about in the article I wrote in our first edition, "The state of quantum computing today"), but they are not without their challenges. In particular, photons are fragile and hard to confine, which is a problem because many of these applications rely on confined photons (e.g. between near-perfectly reflecting mirrors). Furthermore, we still don't have a reliable way of emitting a single photon on-demand, which is crucial for these applications [1]. To do information processing with a small number of photons, we would like to control when and how photons are emitted. Being able to manipulate quantum systems predictably is a huge challenge we face today.

In my research with Professor Howard Carmichael, we're studying a particular driven, two-level open quantum system with a quantum feedback loop to study its behaviour and possible applications to predictable photon pair productions.

A two-level system describes the energy levels of an atom, where the lower level is its ground state, and the higher level is its excited state. The driven part describes a laser that can excite the atom, and this laser takes the atom that is initially in its ground state to its excited state. The atom can spontaneously emit a photon to bring itself back down to the ground state, so we have a situation where the atom continuously gets excited by the laser, emits a photon, and is re-excited again. This is known as resonance fluorescence of a driven two-level atom and has been studied extensively and experimentally realised. This type of resonance fluorescence is seen when the atom is in free space, with no interaction other than the laser.

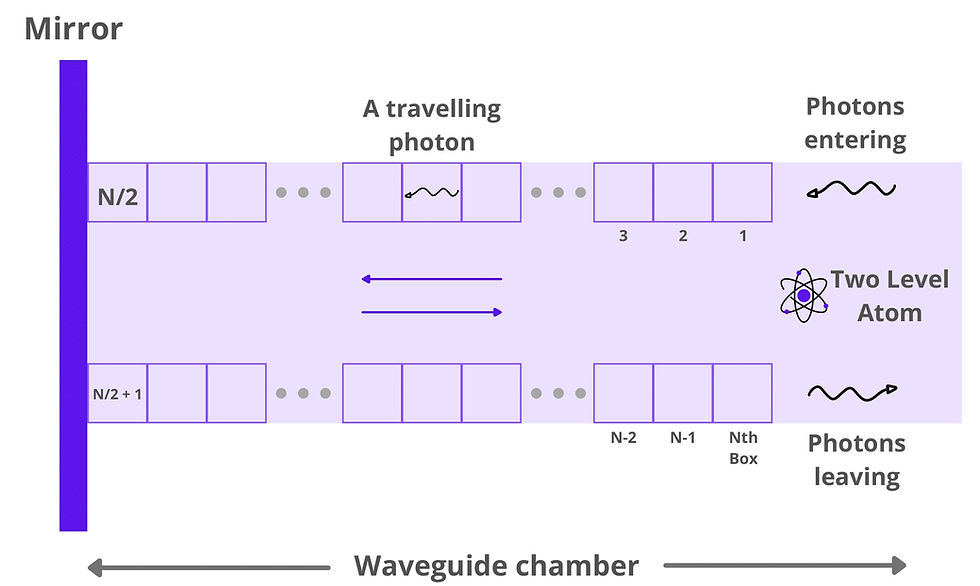
Figure 1

We're adding a little more complexity to this system by implementing a quantum feedback loop in our research. The photons the atom has previously emitted are reflected by a mirror and interact with the atom once again. The general setup is confined in a waveguide (Fig. 1). You can think of the waveguide as simply a chamber that encloses the system, with an output channel. The photon is emitted by the two-level atom, travels to the right, gets reflected by the mirror and travels back to interact with the atom once again before leaving the waveguide to be detected. The entire system is enclosed inside this waveguide.

Even in a relatively simple setup like this, we can observe fascinating behaviours. This is the beauty of physics, where simple systems can result in very elegant physics. One of the most notable behaviours is that we can trap photons in our waveguide and create photon pairs that are emitted together. However, before we can discuss its nature, we first need a way to simulate this quantum system.

Due to the inherently probabilistic nature of quantum systems, we cannot observe the atom directly and make conclusions. To study the behaviour of this open quantum system, we employ a few methods. Firstly we use Quantum Trajectory Theory [2] to simulate these photon emissions. This theory uses a Monte-Carlo type approach to characterising the open quantum system, and we average over many simulations to build a statistical average to understand the system's inner workings. Quantum trajectory theory is a powerful tool because it builds this statistical average by only looking at the system's output, i.e., its environment¹ [3, 4]. We also assume that there are no more than two photons in the waveguide at any given moment. This dramatically reduces the complexity of the simulation to something feasible to compute in an appropriate amount of time. Finally, we use a space-discretised waveguide model (SDWM), where we split the space between the atom and the mirror into small boxes and claim we can not have two photons in any box simultaneously. [5] The basic principle of this simulation is that we evolve the system, and every time step, we shift the boxes by one and look at what is inside the Nth box as seen on Figure 1. The condition for the next time step depends on whether or not a photon was found in the Nth box in the previous time step. We typically average over 50,000 to 100,000 simulations.

If the photons emitted have a pi phase shift relative to the two-level atom, it will destructively interfere with the atom on its round trip back. This creates a system where no photon can leave the waveguide, i.e., photon trapping. However, this is only for the case in which there is only one photon in the waveguide. The story becomes more interesting when two photons are in the waveguide at the same time. In this situation, both photons are let out. In a sense, it is like the second photon in the waveguide lets out the first trapped photon. Both photons leave, and because they were in the waveguide at the same time, they are at most separated by the round trip time. Hence we now have a system that emits photon pairs, which are emitted in a very short time apart.

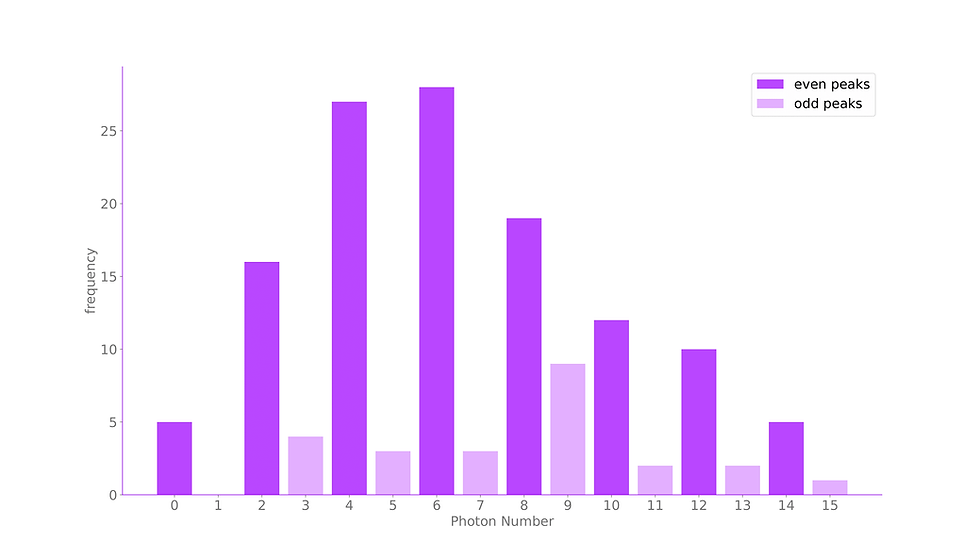
Figure 2

These behaviours can be summarised mainly in photon counting distributions and photon waiting time distributions. Photon counting distributions show a histogram of the number of photons detected in each of the simulations. With the pi phase destructive interference regime, the photon counting distributions mainly only have peaks at even numbers of photons due to the photon pair production. An example of this is shown in Figure 2. There are some odd peaks, which are mostly due to a rare triple photon emission where three photons are emitted together under the round trip time. The physics behind this is yet to be studied. The waiting time distributions show the time distributions between photon emissions, i.e. when a photon is detected, how long do you have to wait until you see another photon? Again in this pi phase shift regime, there are strong peaks below the round trip time and a decaying tail for the rest of the time. Figure 3 shows an example of this waiting time distribution, where there’s a clear peak for waiting times below the round trip time. However, we are still yet to understand the shape of this distribution and the physics behind it properly.

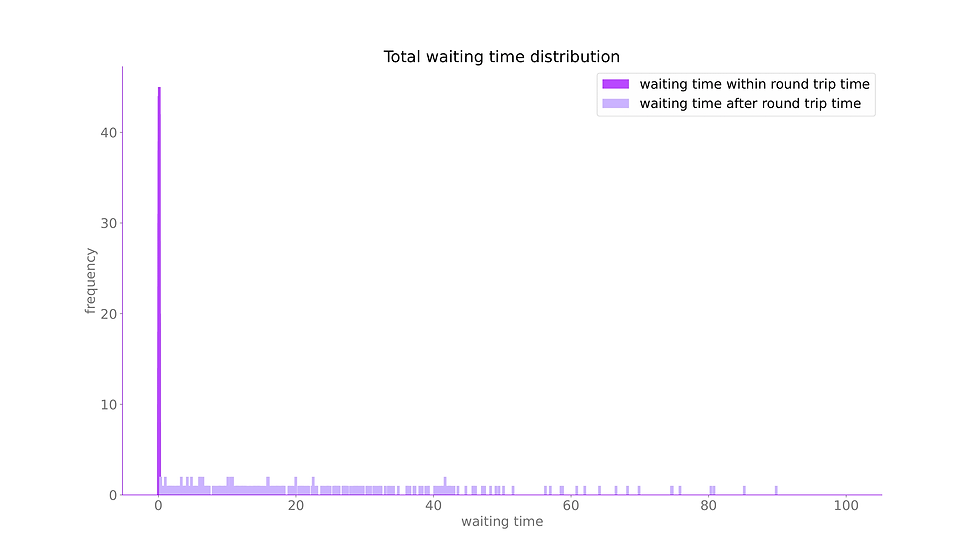
Figure 3

Photons are the universe's fundamental information carriers. We are now transitioning (slowly) to a world where quantum technologies become more ubiquitous. The manipulation and controlling of individual or few photons will be key in utilising the unique properties that the quantum realm brings to the table such as quantum entanglement and quantum tunnelling.

By studying this system, we hope to find ways to use this kind of setup for future quantum information processing applications.

Footnote

1. Quantum trajectory theory has been recently for the first time experimentally realised by a group at Yale. For the last 100 years or so, physicists have thought that the “quantum jump”, that particles make to go to the next energy level, is instantaneous. Quantum trajectory theory predicts that it is in fact possible to predict the path through phase space the atom takes. In this experiment, the group was able to detect an atom changing energy levels, catch the transition mid-flight, and push it back to its original state. If that’s not cool, you’re not cool.

References

1. Lvovsky, A., Sanders, B. and Tittel, W., Optical quantum memory. Nature Photonics, 3(12), pp.706-714, 2009.

2. H. Carmichael, “An Open Systems Approach to Quantum Optics,” Berlin Heidelberg: Springer-Verlag , 1993.

3. P. Ball, “How a new twist on quantum theory could solve its biggest mystery,” New Scientist, 25-Mar-2020. [Online]. Available: https://www.newscientist.com/article/mg24532750-700-how-a-new-twist-on-quantum-theory-could-solve-its-biggest-mystery/.

4. Z. K. Minev, S. O. Mundhada, S. Shankar, P. Reinhold, R. Gutiérrez-Jáuregui, R. J. Schoelkopf, M. Mirrahimi, H. J. Carmichael, and M. H. Devoret, “To catch and reverse a quantum jump mid-flight,” Nature, vol. 570, no. 7760, pp. 200–204, 2019.

5. S. Arranz Regidor, G. Crowder, H. Carmichael, and S. Hughes, “Modeling quantum LIGHT-MATTER interactions in waveguide Qed With retardation, Nonlinear interactions, and a time-delayed feedback: Matrix product states versus a Space-discretized Waveguide model,” Physical Review Research, vol. 3, no. 2, 2021.

Captions

Figure 1. A schematic of the open quantum system we are simulating.

Figure 2. Photon counting distribution of our system. The high peaks at even numbers of photons suggest photon pair productions.

Figure 3. Waiting time distribution of our system. The large peaks seen at times below the round trip time suggest photons are coming out in pairs.